快速排序细节分析

发表于 更新于 分类于 阅读次数： 本文字数： 12k 阅读时长 ≈ 11 分钟

在翻看C++标准库源码的时候，突然发现std::sort的实现和我想的很不一样，并不是简单的快排

在查询了一些资料以后，大致搞明白了这个introsort的原理

这篇写的很好：知无涯之std::sort源码剖析

另外就是STL源码分析那一本写的很好，不是本文的重点，简单过一下，我的gcc版本是5.4.0

introsort原理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
__introsort_loop(_RandomAccessIterator __first,
        _RandomAccessIterator __last,
        _Size __depth_limit, _Compare __comp)
{    
    while (__last - __first > int(_S_threshold))
    {    
        if (__depth_limit == 0)
        {    
            std::__partial_sort(__first, __last, __last, __comp);
            return;
        }    
        --__depth_limit;
        _RandomAccessIterator __cut =
            std::__unguarded_partition_pivot(__first, __last, __comp);
        std::__introsort_loop(__cut, __last, __depth_limit, __comp);
        __last = __cut;
    }    
}    

template<typename _RandomAccessIterator, typename _Compare>
    inline void 
__sort(_RandomAccessIterator __first, _RandomAccessIterator __last,
        _Compare __comp)
{    
    if (__first != __last)
    {    
        std::__introsort_loop(__first, __last,
                std::__lg(__last - __first) * 2, 
                __comp);
        std::__final_insertion_sort(__first, __last, __comp);
    }    
}

introsort先在__introsort_loop中进行传统快排的分区算法和递归，每一轮递归减少__depth_limit

当初始值为lg(__last - __first) * 2,也就是2lgN的__depth_limit归零后，判断快排可能进入了劣化局面，可能会退化为O(N^2)的时间复杂度

因此使用__partial_sort也就是堆排序，最差时间复杂度为O(nlgn)

然后当递归到__last - __first <= _S_threshold(值为16)

那么结束递归，调用__final_insertion_sort做插入排序，因为插入排序在元素较少或大致有序时速度较快

讨论的重点在std::sort使用的快排

std::sort使用的快排

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
template<typename _RandomAccessIterator, typename _Compare>
    _RandomAccessIterator
__unguarded_partition(_RandomAccessIterator __first,
        _RandomAccessIterator __last,
        _RandomAccessIterator __pivot, _Compare __comp)
{
    while (true)
    {
        while (__comp(__first, __pivot))
            ++__first;
        --__last;
        while (__comp(__pivot, __last))
            --__last;
        if (!(__first < __last))
            return __first;
        std::iter_swap(__first, __last);
        ++__first;
    }
}

/// This is a helper function...
template<typename _RandomAccessIterator, typename _Compare>
    inline _RandomAccessIterator
__unguarded_partition_pivot(_RandomAccessIterator __first,
        _RandomAccessIterator __last, _Compare __comp)
{
    _RandomAccessIterator __mid = __first + (__last - __first) / 2;
    std::__move_median_to_first(__first, __first + 1, __mid, __last - 1,
            __comp);
    return std::__unguarded_partition(__first + 1, __last, __first, __comp);
}

我遇到了几个问题，为什么pivot的值进行了一定的选择？

为什么分区算法是双指针，而算法导论上是单指针，另外双指针都没有判范围，这样不会跑挂吗？

根据一些资料查询，这里使用的是三点取中Hoare分区算法

那么回顾一下算法导论的快排，对比一下区别吧

算法导论的快排

单指针分区算法又叫Lomuto分区算法，非常的简单易懂

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
int quick_sort_partion(vector<int> &nums, int start, int end) {
    int pivot = nums[end]; //取尾部为基准值
    int smallerThenPivotIndex = start; //维护一个指针，[0, smallerThenPivotIndex - 1]都 < pivot
    for (int cur = start;cur < end;cur++) {
        if (nums[cur] <= pivot) { 
            //遍历全部值，一旦小于基准值就单指针自增，并且将当前值和指针值交换
            swap(nums[cur], nums[smallerThenPivotIndex]);
            smallerThenPivotIndex++;
        }   
    }   
    //将基准值和维护的指针交换
    swap(nums[end], nums[smallerThenPivotIndex]);
    return smallerThenPivotIndex;
}
void quick_sort_imp(vector<int> &nums, int start, int end) {
    if (start < end) {
        int q = quick_sort_partion(nums, start, end);
        quick_sort_imp(nums, start, q - 1); 
        quick_sort_imp(nums, q + 1, end);
    }   
}
void quick_sort(vector<int> &nums) {
    quick_sort_imp(nums, 0, nums.size() - 1); 
}

Hoare分区算法

双指针算法又叫Hoare分区算法，是设计快排的大佬设计的分区算法

在std::sort的unguarded_partition中，last--没和first++放在一起，是因为last代表着区间的后一个元素，因此需要提前进行一次last--

将last--后置以后，大概是如下算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
int random_quick_sort_partion(vector<int> &nums, int start, int end, int pivotIndex) {
    int pivot = nums[pivotIndex];
    while(true) {
        while(nums[start] < pivot) start++;
        while(nums[end] > pivot) end--;
        if (start >= end) {
            break;
        }
        swap(nums[start], nums[end]);
        start++;
        end--;
    }
    return start;
}
void random_quick_sort_imp(vector<int> &nums, int start, int end) {
    if (start < end) {
        int pivotIndex = (rand() % (end - start)) + start + 1; //rand()%(end-start),结果[0, end - start - 1]
        int q = random_quick_sort_partion(nums, start, end, pivotIndex);
        random_quick_sort_imp(nums, start, q - 1);
        random_quick_sort_imp(nums, q, end);
    }
}
void random_quick_sort(vector<int> &nums) {
    random_quick_sort_imp(nums, 0, nums.size() - 1);
}

这里有几个问题：

1 为什么不需要边界检测？

2 为什么start == end的时候需要break？

3 为什么随机pivot不能取start？

4 为什么返回start作为分隔？end可不可以？

5 为什么Hoare分区后递归的区间和Lomuto分区算法不一样？

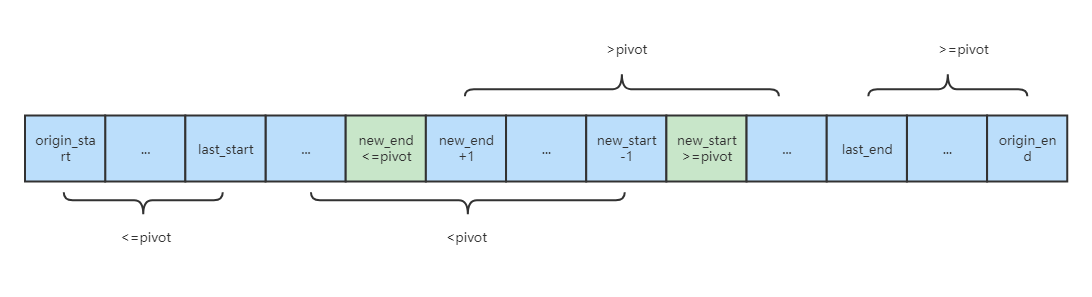
回答这些问题前，先看下这个图

这个图绘制了即将跳出循环的情况

origin_start代表random_quick_sort_partion的参数start，origin_end同理

last_start代表上一轮循环交换时start停留的位置，last_end同理

new_start代表本轮循环start会在哪里停留，new_end同理

1

为什么不需要边界检测？

以start为例进行分析

  • 假设当前是第一轮循环，那么最坏情况下new_start会停在pivot的位置上

  • 假设当前是第N轮循环，那么N-1次循环的时候，last_start和last_end交换的以后，nums[last_end, origin_end]这一段必然>=pivot了

    那么最坏情况下new_start会停在last_end上

end同理，因此不需要边界检测

end的时候需要break？

  • 首先给反例

    假设给一个有序自增且不重复的序列

    pivot_index取origin_end，那么第一轮循环，new_start在[0, origin_end]都不符合要求，会直接跑越界

    pivot_index取origin_start同理，new_end会朝着起点方向越过0跑越界

    如果start == end的时候break，就能防止越界

  • 其次

    start == end的时候，表示这是同一个值，此时swap是冗余操作

为什么随机pivot不能取start？

即使start == end的时候break，随机pivot也不能取start

假设给一个有序自增且不重复的序列，当pivot_index取start的时候，第一轮循环new_start停在origin_start，new_end在[origin_start + 1，origin_end]都不符合要求，也停在origin_start

此时分区算法返回的q为origin_start，那么下一轮quick_sort的递归，会分别计算[origin_start，q - 1] 和 [q，origin_end]

也就是[origin_start，origin_start - 1] 和 [origin_start， orgin_end]，后者和本轮递归的范围一致，会导致无限递归无法收敛

为什么返回start作为分隔？end可不可以？

可以的，观察图片可以得到结论new_start停在>=pivot的值上，new_end停在<=pivot的值上

  • 对start作为分隔来说

    由于[origin_start，new_start - 1]一定<=pivot，所以可以作为一半的分隔

    而[new_end，origin_end] > pivot，new_start >= new_end，因此[new_start，origin_end]作为子集一定也>pivot，所以可以作为另外一半的分隔

    简单的来说new_start可能>pivot，因此在分区算法的右边，返回start时为[start, q - 1],[q, end]

  • 对end作为分隔来说

    由于[new_end + 1，origin_end ]一定>=pivot，所以可以作为一半的分隔

    而[origin_start，new_start] < pivot，new_end <= new_start，因此[origin_start，new_end]作为子集一定也<pivot，所以可以作为另外一半的分隔

    简单的来说new_end可能<pivot，因此在分区算法的左边，返回end时为[start, q],[q + 1, end]

  • 另外，返回end时，随机pivot不能取end：

    假设给一个有序自增且不重复的序列，当pivot_index取end的时候，第一轮循环new_end停在origin_end，new_start在[origin_start ，origin_end - 1]都不符合要求，也停在origin_end

    此时分区算法返回的q为origin_end，那么下一轮quick_sort的递归，会分别计算[origin_start，q] 和 [q + 1，origin_end]

    也就是[origin_start，origin_end ] 和 [origin_end + 1， orgin_end]，第一次递归和本轮递归的范围一致，会导致无限递归无法收敛

因此如果返回end可以这样实现代码

1
2
3
4
5
6
7
8
void random_quick_sort_imp(vector<int> &nums, int start, int end) {
    if (start < end) {
        int pivotIndex = (rand() % (end - start)) + start; // 不同于返回start时, 随机时不能选择end作为pivot_index
        int q = random_quick_sort_partion(nums, start, end, pivotIndex);
        random_quick_sort_imp(nums, start, q); //不同于返回start时
        random_quick_sort_imp(nums, q + 1, end); //不同于返回start时
    }
}

为什么Hoare分区后递归的区间和Lomuto分区算法不一样？

核心原因是因为Hoare分区算法只保证大于pivot和小于pivot的值分隔开，不考虑=pivot的值的位置，当向下递归时，总能保证这一轮递归=pivot的值会放置在该放的位置

而Lomuto分区算法会保证=pivot值在分区完成后一定在他该在的位置，这增加了很多计算量

这也是Hoare分区算法的优势，在序列存在大量相同值时，性能会比Lomuto分区算法好得多

当然这也增加了边界计算时的复杂性，也就是3.3和3.4看到的，会有bad_case导致递归无法收敛而无限递归

new_end最大为1

这是观察图片可以得到的一个额外的有趣结论

由于[last_start + 1, new_start - 1]都小于pivot

而 [new_end + 1, last_end - 1]都大于pivot，由于new_start >= new_end

那么在new_start和new_end之间的数[new_end + 1, new_start - 1]既要大于pivot又要小于pivot

这显然是不可能的，因此new_start最多比new_end大1

我想这也是这个算法性能高的原因，我一开始还担心start++和end--的循环里不做start和end的大小的边界校验，会浪费很多性能

性能测试

测试代码

测试环境

1
2
3
gcc: gcc version 5.4.0 20160609 (Ubuntu 5.4.0-6ubuntu1~16.04.10)
os : ubunut16.04
cpu: Intel(R) Xeon(R) CPU E5-2620 v3 @ 2.40GHz

随机数测试：

100w数据，[0, INT_MAX]全随机

1
2
3
4
5
6
7
8
9
10
11
12
13
14
Lomuto分区算法：
Cost 4473 ms
Hoare分区随机算法：
Cost 3953 ms
stackoverflow抄来的pivot三点取中Hoare分区算法(std::sort使用的快排算法):
Cost 8812 ms
标准库算法:
Cost 4659 ms

杂项：
csdn抄来的奇奇怪怪算法：
Cost 3763 ms
leetcode抄来的奇奇怪怪算法：
Cost 3379 ms

有序数测试：

1w数据，[0, 9999]有序

数据量较少，因为部分测试算法在该用例下时间复杂度过高跑太久了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
Lomuto分区算法：
Cost 2553 ms
Hoare分区随机算法：
Cost 12 ms
stackoverflow抄来的pivot三点取中Hoare分区算法(std::sort使用的快排算法):
Cost 47 ms
标准库算法:
Cost 18 ms

杂项：
csdn抄来的奇奇怪怪算法：
Cost 1889 ms
leetcode抄来的奇奇怪怪算法：
Cost 1880 ms

各个算法在随机数上的情况差不多

但是在顺序数的情况下，Lomuto分区算法在有序数上性能下降明显，Hoare分区随机算法会好很多

pivot三点取中Hoare分区算法的性能会比Hoare分区随机算法低（前者算法胜在稳定，不会因为随机运气特别差而撞到O(n^2)）

而标准库算法在pivot三点取中Hoare分区算法的基础上进一步优化，性能快得多，几乎赶上了Hoare分区随机算法，也就是理想情况下的O(nlgn)复杂度的时间消耗

Hoare分区算法的局限性

根据上面的分析，Hoare算法在各种场景下都完爆了Lumoto算法，那Lumoto算法的意义是什么？

当分区时选到的pivot有重复数字，需要pivot的重复数字在分区后强制有序时，Hoare算法就不能用了，这个场合也很常见，那就是快速选择算法

快速选择算法

用于解topK问题，标准库算法对应std::n_element

快速选择算法只需要找到序列中排第几位的数字，因此不需要完全有序

假设要找到从0开始下标为k的数字

和二分查找的逻辑类似，每次分区后：

  • 当k = 分区算法返回值q，那么直接返回

  • 当k < 分区算法返回值q，那么n_element(nums, start, q - 1)

  • 当k > 分区算法返回值q，那么n_element(nums, q+1, end)

这要求返回q时，这个q所在位置和最终结果位置是一致的

举个例子，Hoare算法后分区的序列为11211，k=4，返回的q为4，然后就直接返回结果为1，但答案应该是2。这里的问题就在于1没有完全顺序。如果用Lumoto算法后，分区的序列为11112，就不可能找错位置

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
inline int lumoto_partition(vector<int>& nums, int start, int end) {
  int smallerThenPivoxIndex = start;
  int pivot = nums[end];
  for (int i = start;i < end;i++) {
	  if (nums[i] <= pivot) {
		  swap(nums[i], nums[smallerThenPivoxIndex]);
		  smallerThenPivoxIndex++;
	  }   
  }   
  swap(nums[smallerThenPivoxIndex], nums[end]);
  return smallerThenPivoxIndex;
}

inline int lumoto_n_element(vector<int>& nums, int k, int start, int end) {
  if (start >= end) {
	  return start;
  }   
  int pivotIndex = rand() % (end - start) + start;
  swap(nums[end], nums[pivotIndex]);
  int q = lumoto_partition(nums, start, end);
  if (k == q) {
	  return q;
  }   
  if (k > q) {
	  return lumoto_n_element(nums, k, q + 1, end);
  }   
  return lumoto_n_element(nums, k, start, q - 1); 
}
int findKthLargest(vector<int>& nums, int k) {
  int index = lumoto_n_element(nums, nums.size() - k, 0, nums.size() - 1);
  return nums[index];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
inline int hoare_partition(vector<int>& nums, int start, int end, int pivotIndex) {
  int pivot = nums[pivotIndex];
  while(1) {
	  while(nums[start] < pivot) start++;
	  while(nums[end] > pivot) end--;
	  if (start >= end) break;
	  swap(nums[start], nums[end]);
	  start++;
	  end--;
  }
  return start;
}

inline int hoare_n_element(vector<int>& nums, int k, int start, int end) {
  if (start >= end) {
	  return start;
  }
  int pivotIndex = rand() % (end - start) + start + 1;
  int q = hoare_partition(nums, start, end, pivotIndex);
  if (k == q) {
	  return q;
  }
  if (k > q) {
	  return hoare_n_element(nums, k, q, end);
  }
  return hoare_n_element(nums, k, start, q - 1);
}

int findKthLargest(vector<int>& nums, int k) {
  int index = hoare_n_element(nums, nums.size() - k, 0, nums.size() - 1);
  return nums[index];
}

上面分别贴了lumoto和hoare的快速选择算法实现

当nums为不重复数组时hoare算法可用，否则必须要用lomoto算法

时间复杂度

随机快速选择算法虽然看起来和快排很像，但是他的时间复杂度是O(n)，但是随机快排则是O(nlgn)

可以做一下简单的推导

  • 假设随机快排每次都进行二分，那么其递归树可以看做是一颗根节点有1个元素（计算n个节点），第二层有2个元素（各计算n/2个节点），叶子节点层为n个元素（1个节点）的完全二叉树

    那么这棵树层高lgn，每一层都计算n个节点，因此是O(nlgn)的时间复杂度

  • 随机快速选择同理，但是第一层计算n个节点，第二层计算n/2个节点，直到叶子节点层

    n + n/2 + n/4 + ... + 1

    根据等比数列公式，一共计算2n次，因此是O(n)的时间复杂度

扩展：中位数的中位数算法

又叫BFPRT算法，是一个理论上的算法，能保证最差情况下O(n)的时间复杂度

是为了解决随机快速选择算法还是有几率遇到badcase退化到O(n^2)

但是实际工程上BFPRT算法实现非常复杂，常数项特别大

因此标准库std::n_element是使用了和std::sort类似的方式，当执行超过对数项深度时，就退化为建堆来解决问题

中位数的中位数算法成屠龙之技（很多人的实现是不对的，没有完成mutual recursion）

记录一些对应参考资料：

总结

本片简单介绍了C++标准库std::sort算法，详细分析了Hoare分区算法的各种细节和优缺点：

  • 优点：
    • 在序列存在大量相同值时，性能会比Lomuto分区算法好得多
  • 缺点：
    • 增加了边界计算时的复杂性，自己写容易存在bad_case导致递归无法收敛
    • 在序列存在相同值时，无法用于快速选择算法

参考资料

上面测试的leetcode算法就来自这一篇

  • 洛穆托与Hoare两种分区方案

  • 使用 Hoare 分区方案的快速排序算法

  • 快速排序算法 – C++、Java 和 Python 实现

  • QuickSort and Hoare Partition

    因为算法导论的Lomuto分区算法先入为主，我总以为分区后，分区的两边必须完全顺序

    这一篇对我帮助很大，让我搞明白了Hoare分区算法We don't even need to worry where the *E* values wind up on any given pass

    To answer the question of "Why does Hoare partitioning work?":

    Let's simplify the values in the array to just three kinds: L values (those less than the pivot value), E values (those equal to the pivot value), and G value (those larger than the pivot value).

    We'll also give a special name to one location in the array; we'll call this location s, and it's the location where the j pointer is when the procedure finishes. Do we know ahead of time which location s is? No, but we know that some location will meet that description.

    With these terms, we can express the goal of the partitioning procedure in slightly different terms: it is to split a single array into two smaller sub-arrays which are not mis-sorted with respect to each other. That "not mis-sorted" requirement is satisfied if the following conditions are true:

    1. The "low" sub-array, that goes from the left end of the array up to and includes s, contains no G values.
    2. The "high" sub-array, that starts immediately after s and continues to the right end, contains no L values.

    That's really all we need to do. We don't even need to worry where the E values wind up on any given pass. As long as each pass gets the sub-arrays right with respect to each other, later passes will take care of any disorder that exists inside any sub-array.

  • How to partition correctly using the median of the first, middle, and last elements?

    上面测试的Stack Overflow算法就来自这一篇

  • 知无涯之std::sort源码剖析

    这一篇主要侧重点在std::sort的快排，太细节太强啦

相关文章
  • 2022-01-14
    缓存与数据库一致性

    缓存与数据库一致性

    本文主要讨论独立缓存（redis等）和数据库的问题，需要和多个服务节点的内存缓存和数据库的问题进行区分

    后者写入数据库以后，因为服务间rpc代价过高（包括失败代价），没办法再通知全部服务的去修改内存缓存，只能让每个服务的内存缓存自己做定时加载

    另外，在正式讨论这个问题之前，必须知道在非强一致性协议下，无法做到完全的一致性，基于缓存的系统必须要容忍有不一致的时刻

    对独立缓存（redis等）和数据库的操作可以分为两类：