Nginx的平滑加权轮询算法

发表于 更新于 分类于 ， ， 阅读次数： 本文字数： 11k 阅读时长 ≈ 10 分钟

首先分析一下我所见过的权重负载均衡算法的平滑性缺点，最后着重分析来自Nginx的默认算法：平滑加权轮询算法（Smooth Weighted Round-Robin ）

平滑性

首先负载均衡算法的平滑性，我认为包含两个重要特征：

  • 在较大的某个时间窗口内一定会访问某些节点：

    违反这个特征，会导致部分节点的使用率过低

    这可以认为是一种稳定性，稳定的访问有权重的节点

  • 不能太过连续访问某些节点

    违反这个特征，会导致部分节点使用率过高，导致过载

随机负载均衡

很容易想到，把全部权重的总和加起来，然后划定range范围进行随机

例如当前有三个权重节点5：2：1，分别的range范围是[0,4],[5,6][7,7]，总和是8，那么rand() % 8就可以得到本次负载均衡的结果

随机的最大问题是不稳定，理想情况下8次访问应该是5：2：1的流量比例，但是随机在时间范围较大时才能达到这个比例

有一定机率，在小范围时间窗口内会造成8：0：0的结果

这显然不满足平滑性的两个性质

轮询负载均衡

随机不稳定，所以需要使用生成稳定序列的轮询算法

最大堆轮询算法（不推荐）

这是我在taf框架中看到的算法，暂时还没在别的地方见过

使用权重建当前权重最大堆，选出最大节点以后，对其当前权重-1，删除这个节点以后重新插入，直到全部归0后，下一轮继续重建最大堆

还是举例三个权重节点5：2：1，那么生成序列和当前权重如下：

当前权重状态： 选出节点
第一轮：5，2，1 权重5节点
4，2，1 权重5节点
3，2，1 权重5节点
2，2，1 权重5节点
1，2，1 权重2节点
1，1，1 权重5节点
0，1，1 权重2节点
0，0，1 权重1节点
第二轮：5，2，1 权重5节点
略 略

可以发现这个算法非常稳定，但是会连续访问最大权重，也就是说如果是权重499：199：99的情况下，会稳定的先访问499权重的节点300次，这个会让节点稳定过载的算法实在过于离谱

加权轮询（WRR）算法

原理如下图：

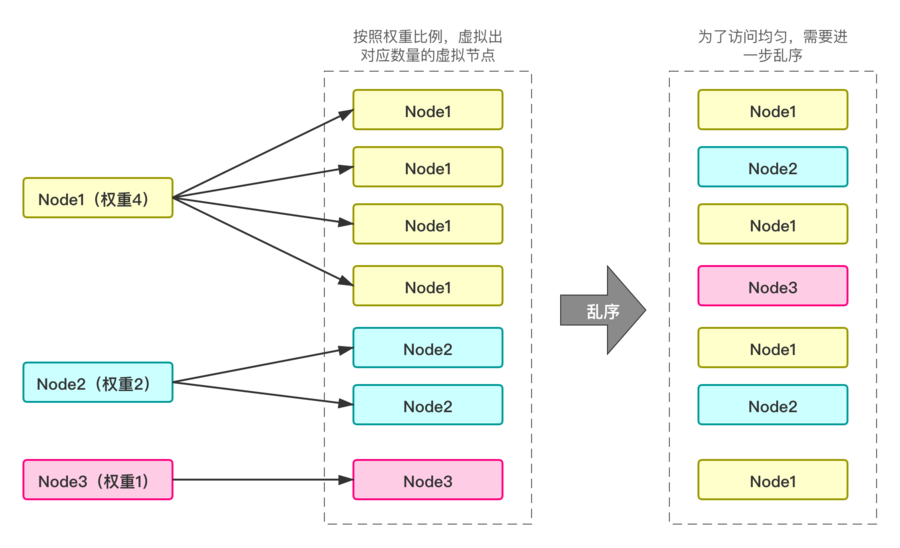
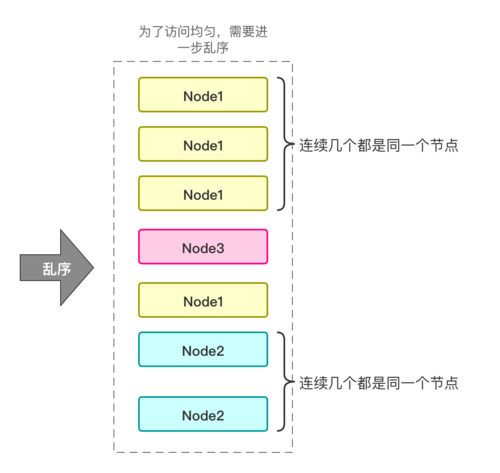
得到图中最右侧的Node列表以后，对其使用普通的RR算法轮询即可，但是打散那一步，面临了随机负载均衡一样的局限性：不稳定

从而违反了平滑性中不能连续访问同一个节点的性质

平滑加权轮询（SWRR）算法

该算法来自 nginx 的一次 commit：Upstream: smooth weighted round-robin balancing

该commit对算法介绍如下：

Algorithm is as follows: on each peer selection we increase current_weight of each eligible peer by its weight, select peer with greatest current_weight and reduce its current_weight by total number of weight points distributed among peers.

也就是说：

  1. 权重累加：每轮选择时，每个可用节点的当前权重（current_weight）增加其自身的配置权重（weight）。
  2. 选择最大权重节点：选择当前权重（current_weight）最大的节点进行负载分配。
  3. 被选中节点的权重调整：选中的节点的当前权重（current_weight）减去总配置权重和（total of weights）。

该commit还举了一个例子，整理如下：

各节点current_weight 权重累加后各节点current_weight 选中节点 被选中节点的权重调整
a(0), b(0), c(0) a(5), b(1), c(1) a a.current_weight = 5 - (5+1+1) = -2
a(-2), b(1), c(1) a(3), b(2), c(2) a a.current_weight = 3 - (5+1+1) = -4
a(-4), b(2), c(2) a(1), b(3), c(3) b b.current_weight = 3 - (5+1+1) = -4
a(1), b(-4), c(3) a(6), b(-3), c(4) a a.current_weight = 6 - (5+1+1) = -1
a(-1), b(-3), c(4) a(4), b(-2), c(5) c c.current_weight = 5 - (5+1+1) = -2
a(4), b(-2), c(-2) a(9), b(-1), c(-1) a a.current_weight = 9 - (5+1+1) = 2
a(2), b(-1), c(-1) a(7), b(0), c(0) a a.current_weight = 7 - (5+1+1) = 0
a(0), b(0), c(0) ...

该commit最后介绍了故障时的处理

To preserve weight reduction in case of failures the effective_weight variable was introduced, which usually matches peer's weight, but is reduced temporarily on peer failures.

为了在发生故障时保留权重的减少，引入了 effective_weight 变量。通常，这个变量与节点的权重相匹配，但在节点故障时会被临时减少。

也就是说，不止存在配置权重（weight），还存在有效权重（effective_weight）

对应代码在这里：https://github.com/nginx/nginx/blob/52327e0627f49dbda1e8db695e63a4b0af4448b1/src/http/ngx_http_upstream_round_robin.c#L491

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
static ngx_http_upstream_rr_peer_t *
ngx_http_upstream_get_peer(ngx_http_upstream_rr_peer_data_t *rrp)
{
    for (i = 0; i < rrp->peers->number; i++) {
        peer = &rrp->peers->peer[i];

        if (peer->down)
            continue; //已经下线的不再参与计算

        if (peer->max_fails
            && peer->fails >= peer->max_fails
            && now - peer->checked <= peer->fail_timeout)
            continue; //错误达到一定数量的不再参与计算

        peer->current_weight += peer->effective_weight;	//权重累加
        total += peer->effective_weight;

        if (peer->effective_weight < peer->weight)
            peer->effective_weight++; //在ngx_http_upstream_free_round_robin_peer中被调低权重的进行恢复

        if (best == NULL || peer->current_weight > best->current_weight)
            best = peer; //选择最大权重节点
    }

    if (best == NULL) {
        return NULL;
    }

    best->current_weight -= total; //被选中节点的权重调整

    return best;
}

void
ngx_http_upstream_free_round_robin_peer(ngx_peer_connection_t *pc, void *data,
    ngx_uint_t state)
{
    if (state & NGX_PEER_FAILED) {
        if (peer->max_fails) {
            peer->effective_weight -= peer->weight / peer->max_fails; //存在失败状态的，降低其权重
        }
        if (peer->effective_weight < 0) {
            peer->effective_weight = 0; //有效权重最少为0
        }
    }
}

证明算法性质

假设有三个服务器节点\(A, B, C\)，它们的配置权重分别为 $weight_A, weight_B, weight_C $ 并保持不变，所有服务器节点配置权重的总和表示为\(weight_{sum} = weight_A + weight_B + weight_C\)

每一次执行完，当前权重和为0

每一次执行后，每个节点的当前权重会分别增加$weight_A, weight_B, weight_C \(，也就是权重和增加\)weight_{sum}\(，随后选出的节点减少\)weight_{sum}$​，因此权重和增长为0

由于初始的\(weight_{sum} = 0\)，而每一次执行完增长为0，所以当前值永远为0

每过权重和值的次数，每个节点被选择配置权重次数

也就是每过\(weight_{sum}\)次负载分配，A节点被选择\(weight_A\)次，B节点被选择\(weight_B\)次，C节点被选择\(weight_C\)​次

  • 首先证明A节点被选择\(weight_A\)次：

    当 \(i\) 次负载分配后，A节点恰好完成了 \(weight_A\) 次的选择，那么此时A节点的当前权重\(current\_weight_A = i * weight_A - weight_A * weight_{sum} = weight_A*(i-weight_{sum})\)

    • 当 \(i = weight_{sum}\)时，\(weight_{sum}\)次选择了\(weight_A\)​次的A节点

    • 当 \(i < weight_{sum}\)时，后续\(weight_{sum} - i\)次最多还能增长\(weight_A * (weight_{sum} - i)\)，和\(current\_weight_A\)加起来正好为0，也就是\(current\_weight_A\)在后续都不可能大于0了

      已知每一次执行完，当前权重和为0，因此每一次执行完后，都会有大于0的\(current\_weight_B\)或者\(current\_weight_C\)

      以第 \(i\) 次负载分配为例，此时的当前权重分别为\(current\_weight_A^i, current\_weight_B^i, current\_weight_C^i\)

      在 \(i+1\) 的负载分配的权重累加阶段，\(current\_weight_A^{i+1} = current\_weight_A^i + weight_A < 0\)

      而\(current\_weight_B^{i+1} = current\_weight_B^i + weight_B > 0 > current\_weight_A^{i+1}\)

      或\(current\_weight_C^{i+1} = current\_weight_C^i + weight_C > 0 > current\_weight_A^{i+1}\)，因此节点A不可能再被选中

    • 那么有没有可能\(i > weight_{sum}\)？

      这意味着\(weight_{sum}\)次的负载分配内，只选择\(weight_A-x\)次的A节点，也就是B或者C共多选择了\(x\)次

      假设B多选择了几次，那么假设当 \(j < weight_{sum}\)时，恰好完成了\(weight_B\) 次的选择，此后\(current\_weight_B < 0\)，不可能再被选中，因此无法被多选

      假设B多选择了几次是不可能发生的，同理C也无法被多选，因此\(i > weight_{sum}\)不成立！

    这意味着A节点最多被选择\(weight_A\)​次，B，C节点也是同理

    因此每个节点最多会被选择对应权重次数

  • 正如在判断当\(i > weight_{sum}\)中讨论的，每过\(weight_{sum}\)次负载分配，某个节点被选择数量小于对应权重的时候，会导致其他节点多选

    因此每个节点最少会被选择对应权重次数

综上可知每个节点只会被选择对应的权重次数

每过W次，每个节点当前权重重新变为0

由上一条可知，每过\(weight_{sum}\)次负载分配，A节点被选择\(weight_A\)次，也就是累加了\(weight_{sum}\)次的权重，并且被选中了\(weight_A\)减少总权重

那么他的当前权重\(current\_weight_A = weight_{sum} * weight_A - weight_A * weight_{sum} = 0\)

B，C节点同理，得证

每个节点不会被连续选择配置权重次数

平滑性不是一个非常准确定义的概念，这里只证明不会被连续选择配置的权重次数

设第 \(i\) 负载分配后A 节点已经被连续选择了 \(weight_A - 1\) 次，那么当前 A 节点的\(current\_weight_A^i\)：

$(weight_A - 1) * weight_A - (weight_A - 1) * weight_{sum} = (weight_A - 1) * (weight_A - weight_{sum}) $

那么在\(i + 1\) 的负载分配的权重累加阶段，\(current\_weight_A^{i+1} = (weight_A - 1) * (weight_A - weight_{sum}) + weight_A\)

由于权重都是正整数，那么\(weight_A - weight_{sum} <= -1\)

代入得到\(current\_weight_A^{i+1} <= (weight_A - 1) * -1 + weight_A = 1\)

而\(current\_weight_B^i\)是累加过\(weight_B\)的，\(i+1\) 的负载分配的权重累加阶段又累加了一次\(weight_B\)

因为\(weight_B\)是正整数，因此\(current\_weight_B^{i+1} >= weight_B * 2 > 1\)

\(current\_weight_B^{i+1} > current\_weight_A^{i+1}\)，不可能再选A节点

缺陷：多实例冷启动造成的流量突增

在QPS 比 Nginx 提升 60%，阿里 Tengine 负载均衡算法揭秘中提到

被调高权重的机器当时被分发到的流量基本上是该应用机房总流量的 1/2，一段时间后该机器的流量才恢复到预期的权重比例。其原因就是由于接入层 Tengine 对后端机器信息的变化是动态感知热生效的，而 Nginx 官方的 SWRR 算法策略第一次会选择当前机器列表中权重最大的机器转发流量。从而进一步导致已感知到后端机器权重变化的接入层 Tengine 都会将第一个请求转发到权重被调高的机器上。

评论中补充了一些信息：

晨光影：

基本上看懂了，但是仍然存在疑惑待解：

单机权重从1调到2，出现一段持续时间的1/2机房流量分配到权重调高的机器？？？

MBSKY：

首先只有权重调整的那一瞬间，被调高权重的机器的流量才会暴涨。原因：在SWRR算法初始状态下会选择机器列表中权重最大的机器转发流量。而Nginx是多进程模型，其中每个worker进程都是独立的按照SWRR算法选取后端机器转发流量的，这就会导致整个机器的流量都会转发到权重被提高的后端机器上。

这里其实没有说清楚Tengine的动态感知热生效机制，所以在其他博文SWRR存在的问题引用了这一段并且说

我在自测过程中，在算法启动后动态调整weight和effective_weight的值是不存在这个问题的，访问依旧均匀，并不会出现大规模pick到加权节点上的情况，个人猜测他们可能是在探听到weight变化后，把对应节点的current_weight也给改掉了才可能出现这个问题。

误解成了在运行到一半的时候，改大了某个节点的effective_weight和weight，SWRR会出现不均衡的情况

根据QPS 比 Nginx 提升 60%，阿里 Tengine 负载均衡算法揭秘中我标记加粗的第一次和初始状态，我认为应当是配置文件在修改了权重以后，触发了Nginx的reload，当时那一台机器的effective_weight被调整到最高，而SWRR的首次调用肯定是先分配流量给最高节点的，多实例Nginx在多进程的模型下，首次调用可能会是一个很大的量级

解决办法

我看到这一篇负载均衡算法WRR介绍中所述

应对这样的问题：我们可以在生成序列之后随机选择一个开始，比如我们有5台负载的机器，它们都生成了a,a,b,a,c,a,a的序列，但是我们不完全按照这个序列轮训，在每台机器上可以随机选择一个开始，那生成的序列就可能变成下面这样：

机器 序列
机器1 a,b,a,c,a,a…
机器2 b,a,c,a,a,a,a…
机器3 a,a,b,a,c,a,a…
机器4 c,a,a,a,a,b,a…
机器5 a,b,a,c,a,a…

这样能降低些第一台机器被爆掉的概率。

这个方法的问题在于，当权重值特别高时需要生成一个很大的序列，并且当节点不停变化新增删除节点的时候，需要不停地重新生成序列，这个方案不够完美

我认为可以在每个节点加入时给\(current_{weight}\)一个初始的随机权重，该权重应当小于总权重和\(weight_{sum}\)，可以简单认为给予一个先发优势，这个优势在第一次分配流量以后，就会因为被减去了\(weight_{sum}\)从而失去优势，也就是说，初始化的随机权重就算胜出，也只能多赢得一次，这里懒得再推导证明公式了，直接写一个代码测试

测试

以下代码模拟了随机初始权重，并且在执行一半的时候某节点故障

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
#include <iostream>
#include <vector>
#include <algorithm>

struct Node {
    std::string name;
    int weight;
    int effective_weight;
    int current_weight;
    int fails;
    bool down;

    Node(std::string n, int w)
        : name(n), weight(w), effective_weight(w), current_weight(0), fails(0), down(false) {}
};

class LoadBalancer {
    public:
    LoadBalancer(const std::vector<Node>& nodes) : nodes_(nodes) {
        srand(time(0));
        int total = 0;
        for (auto &node : nodes_) {
            total += node.effective_weight;
        }
        for (auto &node : nodes_) {
            node.current_weight = rand() % total;
        }
        std::cout << "init:   ";
        for (auto &node : nodes_) {
            std::cout << node.current_weight << '\t';
        }
        std::cout << std::endl;
    }

    void simulate(int initial_rounds, int failure_rounds, int failure_index) {
        std::vector<int> initial_selection_count(nodes_.size(), 0);
        std::vector<int> failure_selection_count(nodes_.size(), 0);

        // Run initial rounds
        for (int i = 0; i < initial_rounds; ++i) {
            Node* selected = selectNode();
            initial_selection_count[selected - &nodes_[0]]++;
        }

        // Induce failure in one node
        nodes_[failure_index].down = true;

        // Run failure rounds
        for (int i = 0; i < failure_rounds; ++i) {
            Node* selected = selectNode();
            if (selected == nullptr) {
                std::cerr << "All nodes are down after failure round " << i + 1 << std::endl;
                break;
            }
            failure_selection_count[selected - &nodes_[0]]++;
        }

        // Output results
        std::cout << "Initial Rounds Results:" << std::endl;
        for (size_t i = 0; i < nodes_.size(); ++i) {
            std::cout << nodes_[i].name << " was selected " << initial_selection_count[i] << " times." << std::endl;
        }

        std::cout << "\nAfter Failure Results:" << std::endl;
        for (size_t i = 0; i < nodes_.size(); ++i) {
            std::cout << nodes_[i].name << " was selected " << failure_selection_count[i] << " times." << std::endl;
        }
    }

    private:
    std::vector<Node> nodes_;

    Node* selectNode() {
        Node* best = nullptr;
        int totalEffectiveWeight = 0;

        for (auto& node : nodes_) {
            if (node.down) {
                continue;
            }

            node.current_weight += node.effective_weight;
            totalEffectiveWeight += node.effective_weight;

            if (best == nullptr || node.current_weight > best->current_weight) {
                best = &node;
            }
        }

        if (best != nullptr) {
            best->current_weight -= totalEffectiveWeight;
        }

        std::cout << best->name;
        for (auto &node : nodes_) {
            std::cout << '\t' << node.current_weight;
        }
        std::cout << std::endl;
        return best;
    }
};

int main() {
    std::vector<Node> nodes = {
        {"Node1", 5},
        {"Node2", 2},
        {"Node3", 1}
    };

    LoadBalancer lb(nodes);

    // Simulate initial rounds, then rounds with Node2 failing
    lb.simulate(8, 6, 1);
}

我认为某个节点故障导致节点摘除，同样会导致当前权重和无法归0，和随机初始权重是一样的，因此顺便一起测试

运行输出：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
init:   3	0	7	
Node1	0	2	8
Node3	5	4	1
Node1	2	6	2
Node2	7	0	3
Node1	4	2	4
Node1	1	4	5
Node1	-2	6	6
Node2	3	0	7
Node1	2	0	8
Node3	7	0	3
Node1	6	0	4
Node1	5	0	5
Node1	4	0	6
Node1	3	0	7
Initial Rounds Results:
Node1 was selected 5 times.
Node2 was selected 2 times.
Node3 was selected 1 times.

After Failure Results:
Node1 was selected 5 times.
Node2 was selected 0 times.
Node3 was selected 1 times.

再次运行输出：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
init:   0	2	6	
Node3	5	4	-1
Node1	2	6	0
Node2	7	0	1
Node1	4	2	2
Node1	1	4	3
Node1	-2	6	4
Node2	3	0	5
Node1	0	2	6
Node3	5	2	1
Node1	4	2	2
Node1	3	2	3
Node1	2	2	4
Node1	1	2	5
Node1	0	2	6
Initial Rounds Results:
Node1 was selected 5 times.
Node2 was selected 2 times.
Node3 was selected 1 times.

After Failure Results:
Node1 was selected 5 times.
Node2 was selected 0 times.
Node3 was selected 1 times.

可以发现，一开始随机是什么组合，在一轮运行以后，就会回到什么组合

随机权重让Node3赢得了第一次流量以后，并没有改变最终的流量分配结果

Node2中途故障后，新的Node1和Node3的比例也没有变大或者变小

参考资料

负载均衡-WRR算法

QPS 比 Nginx 提升 60%，阿里 Tengine 负载均衡算法揭秘

Nginx SWRR 算法解读：本文的证明过程非常简略，而且是错的

负载均衡算法WRR介绍

加权轮询算法(wrr

How to prove the Nginx smoothing weight load balancing algorithm mathematically?